روش میانگین حسابی

در دنیای آمار و تحلیل دادهها، برخی از مفاهیم بهعنوان ابزارهای اساسی برای درک و تفسیر اطلاعات مورد استفاده قرار میگیرند. این مفاهیم به ما کمک میکنند تا از میان مجموعهای از دادهها، نمایی کلی و قابل فهم بهدست آوریم. یکی از این مفاهیم، روشهایی هستند که برای جمعبندی دادهها و ارائه یک مقدار واحد بهعنوان نماینده برای کل مجموعه استفاده میشوند.
روش میانگین حسابی یکی از رایجترین و سادهترین ابزارهایی است که در آمار برای تحلیل دادهها به کار میرود. این روش میتواند اطلاعات مختلف را بهصورت عددی جمعبندی کرده و تصویری کلی از ویژگیهای دادهها ارائه دهد. با این حال، این روش مانند هر ابزار دیگری مزایا و محدودیتهای خاص خود را دارد که در کاربردهای مختلف باید به آن توجه کرد.
در این مقاله، به بررسی روش میانگین حسابی، کاربردها و مزایای آن، و همچنین محدودیتهایی که ممکن است در برخی شرایط ایجاد کند، خواهیم پرداخت. این تحلیل به شما کمک خواهد کرد تا درک بهتری از نحوه استفاده از این روش در تحلیلهای آماری داشته باشید.
کاربردهای میانگین حسابی در آمار
میانگین حسابی بهعنوان یکی از ابزارهای پایهای در آمار، کاربردهای متعددی در تحلیل دادهها دارد. این روش در موقعیتهای مختلف به محققان و تحلیلگران کمک میکند تا بهطور مؤثری نتایج را خلاصهسازی کرده و الگوهای موجود را شناسایی کنند. در این بخش به بررسی برخی از مهمترین کاربردهای آن خواهیم پرداخت.
- تحلیل مجموعههای داده بزرگ: در مواردی که حجم زیادی از دادهها وجود دارد، میانگین حسابی میتواند بهعنوان یک نماینده از دادههای موجود عمل کند و روند کلی را نشان دهد.
- مقایسه نتایج مختلف: با استفاده از میانگین حسابی، میتوان نتایج مختلف یک آزمایش یا بررسی را با هم مقایسه کرده و به نتیجهگیریهای مشخصی رسید.
- ارزیابی عملکرد: در تحلیل عملکرد اقتصادی، مالی یا هر زمینه دیگر، میانگین حسابی بهعنوان ابزاری برای ارزیابی میانگین عملکرد در بازههای زمانی مختلف مورد استفاده قرار میگیرد.
- پیشبینی و مدلسازی: در مدلهای آماری و پیشبینی، میانگین حسابی بهعنوان یک مقدار مرکزی میتواند برای پیشبینی روندهای آتی استفاده شود.
- تحلیل تغییرات و نوسانات: با محاسبه میانگین در بازههای زمانی مختلف، میتوان نوسانات و تغییرات در دادهها را بررسی کرد و به نتیجهگیریهای دقیقتری دست یافت.
در نهایت، میانگین حسابی ابزاری است که در بسیاری از زمینهها برای سادهسازی تحلیلهای آماری و تصمیمگیریهای مختلف استفاده میشود. شناخت کاربردهای آن میتواند به تحلیلگران در تصمیمگیریهای دقیقتر و بهموقعتر کمک کند.
چگونه میانگین حسابی محاسبه میشود؟
محاسبه میانگین حسابی فرآیندی ساده و مستقیم است که بهمنظور بهدست آوردن نمایی کلی از مجموعهای از دادهها انجام میشود. این محاسبه بهطور معمول شامل جمعآوری تمامی مقادیر و تقسیم آنها بر تعداد کل دادهها است. در این بخش، مراحل دقیق انجام این محاسبه و اصول پایهای آن را بررسی خواهیم کرد.
برای محاسبه میانگین حسابی، مراحل زیر را باید دنبال کرد:
- جمعآوری دادهها: ابتدا باید تمامی مقادیر موجود در مجموعه دادهها را جمعآوری کرد. این مقادیر ممکن است شامل تعداد زیادی عدد باشند که باید بهطور کامل در نظر گرفته شوند.
- جمع مقادیر: تمامی مقادیر دادهها باید با یکدیگر جمع شوند تا مجموع کلی بهدست آید. این مجموع میتواند هر نوع داده عددی باشد.
- تقسیم بر تعداد دادهها: پس از محاسبه مجموع مقادیر، باید مجموع به تعداد کل دادهها تقسیم شود. این کار بهطور معمول با استفاده از فرمول زیر انجام میشود: میانگین = مجموع مقادیر ÷ تعداد دادهها
بهعنوان مثال، اگر پنج عدد ۲، ۴، ۶، ۸ و ۱۰ داشته باشیم، مجموع این اعداد برابر با ۳۰ خواهد بود. سپس این عدد را بر ۵ (تعداد دادهها) تقسیم میکنیم که نتیجه آن ۶ میشود. بنابراین میانگین حسابی این مجموعه برابر با ۶ خواهد بود.
این روش برای مجموعههای کوچک و بزرگ دادهها قابل استفاده است و یکی از سادهترین و سریعترین روشها برای تحلیل و تفسیر دادهها بهشمار میآید.
مزایا و معایب میانگین حسابی
میانگین حسابی یکی از رایجترین ابزارهای آماری است که برای جمعبندی و تحلیل دادهها استفاده میشود. این روش بهدلیل سادگی و کارایی بالا در بسیاری از موقعیتها مورد توجه قرار میگیرد، اما مانند هر ابزار آماری دیگری، دارای مزایا و معایب خاص خود است. در این بخش، به بررسی برخی از این مزایا و معایب خواهیم پرداخت.
مزایا
- سادگی محاسبه: یکی از مهمترین مزایای میانگین حسابی این است که محاسبه آن بسیار ساده است و نیاز به پیچیدگیهای ریاضی ندارد. این امر آن را به ابزاری سریع و کاربردی برای تحلیل دادههای بزرگ تبدیل میکند.
- توضیحدهی واضح: میانگین حسابی بهراحتی میتواند نمایی کلی از یک مجموعه داده را نشان دهد، که این امر باعث میشود نتایج بهطور قابل فهم و ساده برای مخاطبان مختلف قابل توضیح باشد.
- استفاده در دادههای متنوع: میانگین حسابی میتواند در بسیاری از زمینهها و انواع دادهها بهکار رود، از جمله در دادههای مالی، آموزشی و تحقیقاتی.
معایب
- حساسیت به دادههای پرت: یکی از معایب اصلی میانگین حسابی این است که به دادههای پرت یا مقادیر خیلی بزرگ یا کوچک حساس است. وجود چند داده غیرمعمول میتواند میانگین را بهشدت تغییر دهد و تصویر نادرستی از مجموعه دادهها ارائه دهد.
- عدم نمایش توزیع دادهها: میانگین حسابی تنها یک مقدار مرکزی را نشان میدهد و اطلاعاتی در مورد توزیع دادهها یا تغییرات آنها فراهم نمیکند. این امر میتواند منجر به نتایج ناقص در تحلیلهای پیچیدهتر شود.
- مناسب نبودن برای دادههای غیرخطی: در مواقعی که دادهها بهطور غیرخطی توزیع شدهاند، میانگین حسابی ممکن است نتواند نمای خوبی از وضعیت کلی مجموعه دادهها ارائه دهد.
در نهایت، انتخاب میانگین حسابی بهعنوان ابزاری برای تحلیل دادهها باید با در نظر گرفتن مزایا و معایب آن و همچنین نوع دادههای موجود انجام شود. در شرایط خاص، ممکن است استفاده از سایر روشهای آماری جایگزین مناسبتر باشد.
مقایسه میانگین حسابی با سایر معیارها
در تحلیل دادهها، علاوه بر میانگین حسابی، معیارهای آماری دیگری نیز برای جمعبندی و تحلیل اطلاعات وجود دارند. هر کدام از این معیارها ویژگیها و کاربردهای خاص خود را دارند. در این بخش، مقایسه میانگین حسابی با برخی از مهمترین این معیارها بهمنظور درک بهتر از ویژگیها و تفاوتهای آنها انجام میشود.
مقایسه میانگین حسابی و میانه
میانه یکی از معیارهای مهم برای تحلیل دادهها است که بهویژه زمانی که دادهها شامل مقادیر پرت یا غیرمعمول باشند، مورد استفاده قرار میگیرد. برخلاف میانگین حسابی که بهتمامی مقادیر حساس است، میانه مقدار وسط دادهها را نشان میدهد و به تغییرات ناگهانی و دادههای پرت حساسیت کمتری دارد. به همین دلیل، در مواردی که دادهها نرمال توزیع نشدهاند یا شامل مقادیر افراطی هستند، میانه میتواند نمای بهتری از وضعیت کلی دادهها ارائه دهد.
مقایسه میانگین حسابی و مد
مد بهعنوان مقدار پر تکرارترین داده در یک مجموعه شناخته میشود. این معیار میتواند در موقعیتهایی که دادهها ویژگی خاصی دارند، مانند توزیعهای غیرنرمال یا دستهبندیهای خاص، کاربردیتر از میانگین حسابی باشد. در صورتی که میانگین حسابی نمایی از همه دادهها میدهد، مد تنها به دادههایی که بیشترین تکرار را دارند توجه میکند. این ویژگی باعث میشود که مد در تحلیل دادههای گسسته یا دستهبندی شده نسبت به میانگین حسابی مفیدتر باشد.
در مجموع، انتخاب معیار مناسب برای تحلیل دادهها به ویژگیهای دادهها و هدف تحلیل بستگی دارد. هر کدام از این معیارها، از میانگین حسابی گرفته تا میانه و مد، کاربردهای خاص خود را دارند که با توجه به نوع دادهها و شرایط موجود باید انتخاب شوند.
نقش میانگین حسابی در تحلیل دادهها
میانگین حسابی بهعنوان یکی از ابزارهای کلیدی در تحلیل دادهها بهویژه در زمینههای آماری، اقتصادی و اجتماعی شناخته میشود. این معیار بهطور عمده برای ارزیابی و بررسی ویژگیهای اصلی یک مجموعه داده استفاده میشود. در این بخش، نقش میانگین حسابی در تحلیل دادهها و نحوه تأثیرگذاری آن بر نتایج مختلف مورد بررسی قرار میگیرد.
ارائه نمای کلی از دادهها
یکی از نقشهای اصلی میانگین حسابی در تحلیل دادهها، ارائه یک نمای کلی و ساده از مجموعهای پیچیده از دادهها است. این ابزار به تحلیلگران کمک میکند تا بهطور سریع و کارآمد یک مقدار مرکزی برای دادهها بدست آورند و بتوانند روند کلی اطلاعات را درک کنند. این ویژگی میانگین حسابی بهویژه زمانی مفید است که تحلیلگر بخواهد بدون در نظر گرفتن جزییات جزئی، یک خلاصهبرداری از مجموعه دادهها داشته باشد.
مقایسه و تحلیل روندها
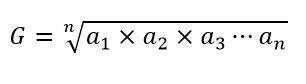
در تحلیلهای آماری و مقایسهای، میانگین حسابی بهعنوان ابزاری برای مقایسه میانگین دادهها در بازههای مختلف یا میان گروههای مختلف استفاده میشود. بهعنوان مثال، در تحلیل روندهای زمانی، میانگین حسابی میتواند تغییرات میانگین در طول زمان را نشان دهد و به تحلیلگر کمک کند تا روندهای رو به رشد یا کاهش را شناسایی کند. این امر در بررسی عملکرد مالی، اقتصادی یا حتی در تحلیل رفتار مصرفکننده مفید است.
با وجود سادگی، میانگین حسابی همچنان ابزاری مؤثر برای تحلیل دادهها در بسیاری از حوزهها است. البته در برخی شرایط خاص، نیاز به استفاده از معیارهای دیگری مانند میانه یا مد بهمنظور بهدست آوردن نتایج دقیقتر و جامعتر احساس میشود.
مثالهای عملی از استفاده میانگین حسابی
میانگین حسابی در بسیاری از حوزهها بهعنوان یک ابزار مفید و کاربردی برای تحلیل دادهها استفاده میشود. در این بخش، چند مثال عملی از کاربرد میانگین حسابی در موقعیتهای مختلف ارائه میدهیم تا بهتر درک کنیم که چگونه این معیار میتواند در مسائل واقعی مورد استفاده قرار گیرد.
در زیر یک جدول نمونه از نمرات دانشآموزان در یک امتحان آورده شده است. با استفاده از این دادهها، میتوانیم میانگین نمرات را محاسبه کنیم تا تصویر کلی از عملکرد دانشآموزان در این امتحان بهدست آوریم.
| نام دانشآموز | نمره |
|---|---|
| Ali | 18 |
| Reza | 15 |
| Sara | 20 |
| Leila | 17 |
| Mohammad | 19 |
برای محاسبه میانگین نمرات، تمامی نمرات را جمع کرده و سپس بر تعداد دانشآموزان تقسیم میکنیم:
میانگین = (18 + 15 + 20 + 17 + 19) ÷ 5 = 17.8
بنابراین، میانگین نمرات این پنج دانشآموز برابر با 17.8 است. این مقدار میتواند بهعنوان یک نمای کلی از عملکرد گروه استفاده شود.
در مثال دیگری، فرض کنید که یک شرکت میخواهد میانگین درآمد ماهانه خود را محاسبه کند تا تصمیمات بهتری در زمینه مالی اتخاذ کند. درآمد ماهانه شرکت در پنج ماه گذشته به شرح زیر است:
| ماه | درآمد (میلیون تومان) |
|---|---|
| فروردین | 50 |
| اردیبهشت | 55 |
| خرداد | 60 |
| تیر | 65 |
| مرداد | 70 |
برای محاسبه میانگین درآمد، مجموع درآمدها را جمع کرده و بر تعداد ماهها تقسیم میکنیم:
میانگین درآمد = (50 + 55 + 60 + 65 + 70) ÷ 5 = 60
در اینجا، میانگین درآمد ماهانه شرکت برابر با 60 میلیون تومان است. این اطلاعات میتواند به شرکت کمک کند تا روند مالی خود را تحلیل کرده و تصمیمات بهتری برای آینده اتخاذ کند.